This article is my take on an Artificial Neuron or Perceptron.
A lot of jargon has been skipped to make concepts easy to understand (or so I believe :p).
Since Logic Gates are easy to solve so I have used, not Python/R/Java/Ruby/
It is simple, easy to use and worked just fine for my work.
Problem Statement :
I am feeling very lazy but my friend invited me to play action cricket, so in order to skip the game I told him that I am happy to play action cricket if:
- I Am able to find my cricket bat
- I get a ride to stadium on a Unicorn
Notes: I am happy to go to cricket stadium without my bat, so this is optional because I can easily borrow one from the other players.
But, Unicorn is non-negotiable/mandatory!.
So let’s solve this:
- Boolean logic
If I have a bat then Input1 is equal to 1 else it is equal to 0.
If I have a Unicorn then Input2 is equal to 1 else it is equal to 0.
If I have a bat and a Unicorn then Input1 and Input2 both are equal to 1.
- Identify things that influence the output:
Point1 or Input1 has no/minimum influence on output (it is optional): so it has less importance or “Weightage”.
So input1 will have a small weight attached to it and I am going to call this weight-one and will give it a value of “1”.
Point2 or Input2 has high influence on output (it is mandatory): so it has high importance or “Weightage”.
So input2 will also have a weight attached to it and I am going to call this weight-two and will give it a value of “5” (a value noticeably higher than weight-one).
- Formula
So the formula for above condition will be :
1
Sum = (Input One * Weight One) + (Input Two * Weight Two)
I am also adding a rule that I will go only if the above Sum is greater than a value let’s say “4” (if sum > 4 then I will go to play cricket).
If input2 is 0 then sum of (input one *weight one) will never reach a value greater than one, so any higher value should work I randomly choose “4”.
Now as per above if the sum is greater than 4 (sum > 4) then I will play.
Or I can say if sum + (-4) is greater than 0 (sum + (-4) >0) then I will play.
This value “-4” is called Bias.
If bias is higher/positive it will be easy to get output greater than 0, if bias is negative then it will be difficult to get output greater than 0.
In my case Bias is negative to make it difficult for output to be greater than 0 (things we do to avoid doing stuff :p).
So as per above if
1
2
3
Output = Sum +Bias > 0 then output is 1/true/i am playing cricket.
Else
Output = Sum +Bias ≤ 0 then output is 0/false/i am not playing cricket.
 Threshold Formula
Threshold Formula
We can now use the above formula to calculate output.
We have already assigned values to weight-one, weight-two and bias.
So if :
I have no bat and no unicorn (0, 0) then output should be 0 (no cricket)
I have no bat but a unicorn (0, 1) then output should be 1(play cricket)
I have a bat but no unicorn (1, 0) then output should be 0 (no cricket)
I have a bat and a unicorn (1, 1) then output should be 1 (play cricket)

Verify Logic
And this is how you train one Artificial Neuron.
Wait, what?
Yea, let’s have a look at the pictorial representation of an Artificial Neuron:
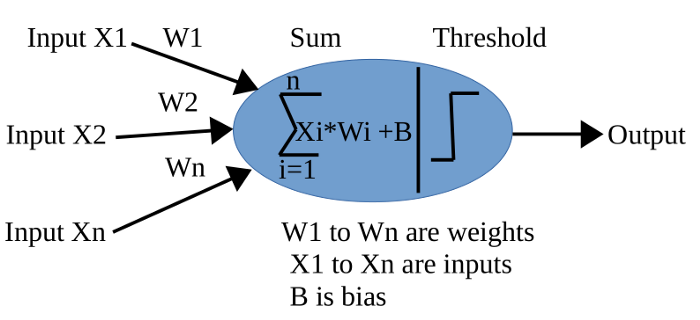
An Artificial Neuron requires:
1
2
3
4
Weight
Input
Bias
Threshold formula : (in above case if sum > 0 then 1 else 0)
We train it by modifying weights until we get the desired output.
An Artificial Neuron is also known as Perceptron.
Next I will train single and multi-layer Perceptrons to solve Logic Gates.
Logic Gates
Training an Artificial Neuron to calculate AND gate.
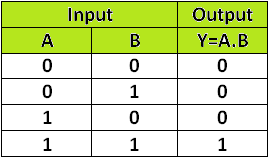
As per above truth table we have two inputs and one output.
To train a neuron we will use above two inputs, assign random weights and a bias and will update the weights (train the neuron) until we get the desired results.
I started with below sheet
(since I have not adjusted the weights so output is incorrect right now)

Since I am going to train only one neuron so weights will be same for all inputs and I will have only one bias, so I merged the weights and bias column.

A positive bias is too high for this Neuron, it is pushing output to one very quickly and for all scenarios so I am going to make it Negative.

Now to see how far we are from the correct output, I am going to calculate error using “Sum Of Squared Errors” formula:
1
SSE =(Take sum of all (Current Output — Expected Output)² )/2
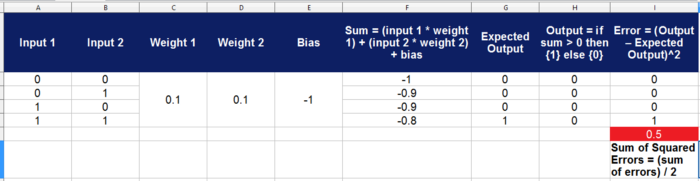
SSE helps me check how much “off” I am, I then use it to update weights.
After playing around with weights, the below are values that gave the correct output.

So as per above values, for an Artificial Neuron to solve AND gate its :
1
2
3
Weight One should be: 0.51
Weight Two should be: 0.1
Bias should be: -1
Training an Artificial Neuron to calculate NAND gate.
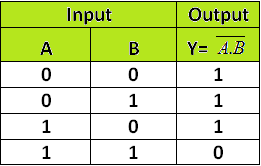
I used the above sheet, used SSE to calculate values to train a Neuron for NAND Gate.

NAND gate is important because it is an Universal Gate, meaning we can solve other Gates using NAND Gate, example XOR Logic Gate
XOR Logic Gate when created using NAND Gates looks like this:
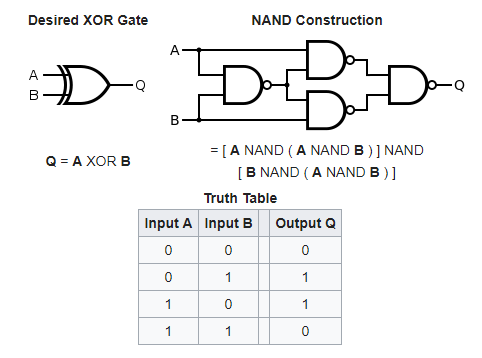
Now we have already trained one neuron to solve for NAND gate.
As per above the NAND to XOR requires four NAND Gates.
So I will use four NAND gate trained neurons that are connected to each other to get a Multi-Layer Artificial Neural Network that is trained to solve XOR Gate.
Mult-Layer Artificial Neural Network
Since I am using NAND trained Neurons to solve XOR, so the Multi-Layer Neural Network will look same as above NAND to XOR diagram.
The only difference is that NAND Gate symbol has been replaced with Neuron symbol.
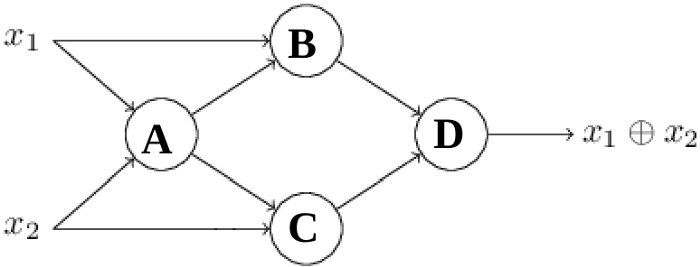
As per above Neuron connections:
1
2
3
4
5
6
Four NAND trained neurons are used.
The trained neurons are connected exactly as per NAND to XOR logic gate diagram.
Inputs X1 and X2 are connected to neuron A, B, C.
Output of neuron A is connected to input of neuron B and C.
Output of neuron B, C is connected to neuron D.
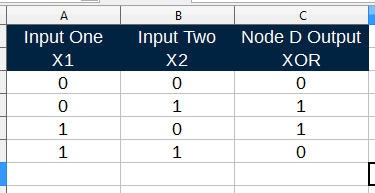
D produces the final output which is X1 Xor X2.
Calculations :
Send Inputs to NAND trained neuron to calculate NAND
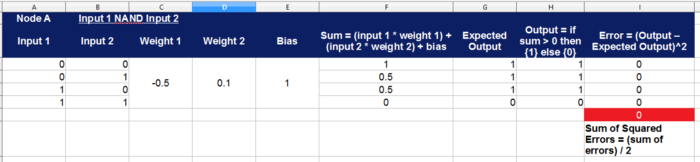
Send Input One and Output of neuron A as inputs to Node B
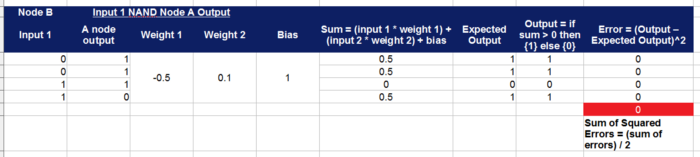
Send Input Two and Output of neuron A as inputs to Node C
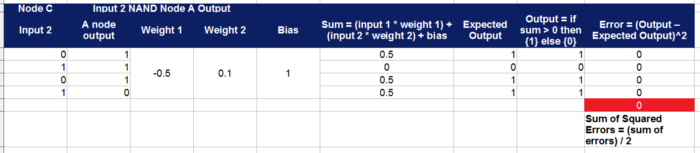
Send output of neuron B and C as inputs to Node D
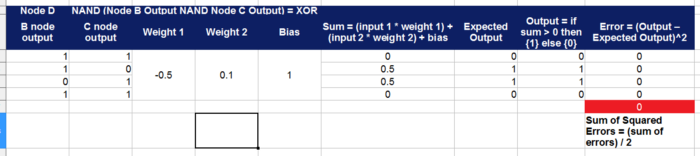
Output of Node D matches the XOR gate result.
That’s all folks!
Excel Sheets
References: